Visible Surface Determination/ Penentuan Permukaan Terlihat

Pendahuluan

Sebagian besar rendering (pembuatan gambar yang lebih realistis) adalah permukaan terlihat masalah, yaitu, hanya menampilkan permukaan mereka yang harus terlihat.



Ini adalah salah satu bidang utama kegiatan dalam komputer grafis dan banyak algoritma yang berbeda dikembangkan. The algorithms can be divided into two classes: Algoritma dapat dibagi menjadi dua kelas:

object space ------------> World Coordinates ruang objek ------------> Koordinat Dunia
image space ------------> PDC Coordinates ruang gambar ------------> PDC Koordinat

Permukaan Tersembunyi Algoritma biasanya ruang gambar atau kombinasi gambar obyek dan ruang. Di bawah ini akan dibahas beberapa dari banyak algoritma penentuan permukaan terlihat.

Kembali Face Penghapusan

Ruang objek sederhana algoritma adalah Back-Face penghapusan (atau wajah kembali menyisihkan) di mana tidak ada wajah-wajah di belakang objek ditampilkan. Karena pada umumnya sekitar setengah dari objek wajah wajah kembali algoritma ini akan menghapus sekitar setengah dari total poligon dalam gambar.
Lihatlah tangan kiri sistem tampilan

Jika C> 0 maka N adalah dalam arah + z, dan wajah-wajah itu menjauh dari VRP, oleh karena itu, jika C> 0 maka itu adalah wajah kembali (untuk sistem tangan Waktu).


Hal ini justru sebaliknya kondisi untuk sistem tampilan tangan kanan.

Jadi algoritma (untuk sistem dengan tangan Waktu):

1. Menghitung N untuk setiap wajah Obyek
2. Jika C (z komponen)> 0 maka wajah kembali dan tidak menarik

Perhatikan bahwa kita harus mampu mengidentifikasi poligon untuk objek.

Metode sederhana ini hanya benar untuk sebuah proyeksi ortografi. Untuk proyeksi perspektif, itu adalah sedikit lebih rumit. Untuk adegan di bawah ini, permukaan yang terlihat berbeda untuk proyeksi ortografi atau perspektif. Para pihak akan terlihat untuk proyeksi ortografi, tetapi tidak untuk proyeksi perspektif.

Untuk proyeksi perspektif, kita harus menentukan apakah Pusat Proyeksi (COP) adalah di dalam atau di luar pesawat dari objek poligon. Jika di dalam COP maka pesawat itu tidak terlihat, jika COP berada di luar maka terlihat.

Ada dua metode untuk menghitung ini:

1. Masukkan COP ke pesawat persamaan dan menentukan apakah di dalam atau di luar. Catatan: pesawat harus menghitung persamaan sebelum transformasi perspektif.
2.Jika sudut antara pesawat normal (N) dan vektor dari setiap titik di pesawat ke COP, V adalah> 90 ° (N · V <0) maka pesawat itu tidak terlihat.

Batasan muka Kembali penghapusan algoritma

1. Itu hanya dapat digunakan pada benda padat dimodelkan sebagai poligon mesh. Ini adalah model yang paling umum untuk membangun sistem grafis garis scan. Bahkan jika objek didefinisikan dalam cara yang berbeda, misalnya dengan parametrik kubik patch atau persamaan implisit, yang biasanya renderer mengkonversi segala sesuatu untuk poligon untuk membuat.
2. cembung polyhedra tetapi belum tentu untuk cekung polyhedra seperti yang ditunjukkan di bawah ini pada contoh dari sebagian wajah tersembunyi, yang tidak akan dihapuskan oleh-wajah Kembali penghapusan.


Bahkan jika kita menggunakan algoritma lain untuk penentuan permukaan terlihat, bagian belakang-wajah menyisihkan yang baik langkah pra-pemrosesan., Setelah menyingkirkan sekitar setengah dari poligon dalam adegan. Juga, untuk warna pelindung kita harus menghitung normal untuk semua poligon tetap.

Penentuan Permukaan Terlihat

Algoritma pelukis didasarkan pada kedalaman menyortir dan merupakan gabungan objek dan citra ruang algoritma. Ini adalah sebagai berikut:

1. Urutkan semua poligon sesuai dengan nilai z (objek spasi); sederhana untuk menggunakan nilai z maksimum
2. Menarik poligon dari belakang (maksimum z) ke depan (minimum z)

Ini dapat digunakan untuk gambar gambar rangka juga oleh berikut:

1. Draw padat poligon menggunakan Polyscan (dalam warna latar belakang) yang diikuti oleh Polyline (poligon warna).
2. Polyscan menghapus Poligon belakangnya kemudian Polyline menarik Polygon baru.

Masalah dengan sederhana Algoritma Painter

Lihatlah kasus di mana tidak bekerja dengan benar. S memiliki kedalaman yang lebih besar daripada S 'dan seterusnya akan diambil terlebih dahulu. Tapi S 'harus digambar terlebih dulu karena dikaburkan oleh S. Kita harus menyusun ulang entah bagaimana S dan S'.:

Kami akan melakukan serangkaian tes untuk menentukan, jika dua poligon perlu mengatur kembali. Jika poligon gagal tes, maka tes berikutnya harus dilakukan. Jika semua tes gagal poligon, maka mereka mengatur kembali. Tes awal komputasi murah, tetapi kemudian tes lebih mahal.

Jadi lihat direvisi algoritma untuk menguji untuk kemungkinan penataan kembali

Dapat menyimpan Zmax, Zmin untuk setiap Polygon.
- Sort pada Zmax
- Mulai dengan poligon dengan kedalaman terbesar (S)
- Bandingkan S dengan semua poligon (P) untuk melihat apakah ada tumpang tindih kedalaman (Test 0)
Jika S. Zmin <= P. Zmax kemudian memiliki kedalaman tumpang tindih (seperti di atas dan di bawah angka)

Jika memiliki kedalaman tumpang tindih (gagal Test 0) kita mungkin perlu untuk menyusun ulang poligon.

memeriksa untuk melihat apakah poligon tumpang tindih dalam bidang xy (gunakan melompat persegi panjang)

Apakah tes di atas untuk x dan y

Jika ada kasus 1 atau 2 maka kita selesai (lulus Tes 1), tetapi untuk kasus 3, kita perlu pengujian lebih lanjut gagal Test 1)

Next test (Test 2) untuk melihat apakah poligon S adalah "di luar" dari poligon (relatif untuk melihat pesawat)

Remember: a point (x, y, z) is Ingat: sebuah titik (x, y, z) adalah "di luar" dari sebuah pesawat jika kita meletakkan titik itu ke dalam pesawat persamaan dan mendapatkan:

Ax + By + Cz + D> 0

Jadi untuk menguji untuk S di luar P, menempatkan semua simpul S ke dalam pesawat persamaan untuk P dan periksa bahwa semua simpul memberikan hasil yang> 0.

yaitu Ax '+ Dengan' + Cz '+ D> 0 x', y ', z' adalah S simpul

A, B, C, D adalah dari pesawat persamaan P (pilih normal menjauh dari pandangan pesawat sejak define "luar" yang berkaitan dengan tampilan pesawat)





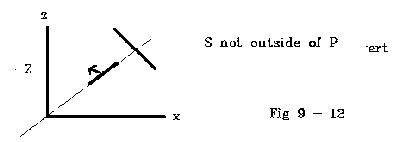
Jika tes S "di luar" P gagal, maka tes untuk melihat jika P adalah "dalam" S (lagi yang berkaitan dengan pesawat melihat) (Tes 3).

Pesawat menghitung persamaan dari S dan dimasukkan ke dalam semua simpul P, jika semua simpul dari P dalam S maka P di dalam.

dalam test: Ax '+ Dengan' + Cz '+ A & lt0 di mana x', y ', z' adalah koordinat dari P simpul

jadi untuk kasus diatas:




Kemudian kita melakukan tes ke-4 dan memeriksa tumpang tindih untuk proyeksi aktual dalam bidang xy karena mungkin telah berlari tumpang tindih empat persegi panjang namun tidak aktual tumpang tindih

Sebagai contoh: Lihatlah proyeksi dua poligon dalam bidang xy

Kemudian ada dua kemungkinan kasus.





All 4 tes gagal karena itu pertukaran P dan S dan scan mengkonversi P sebelum S. Namun sebelum kita scan mengkonversi P kita harus menguji P terhadap semua poligon lain. Lihatlah contoh dari beberapa Persimpangan



Tes S1 melawan S2 dan gagal semua tes begitu menyusun ulang: S2, S1, S3

Test S2 against S3 and it fails all tests so reorder: S3, S2, S1 Tes S2 dan S3 terhadap semua tes gagal jadi menyusun ulang: S3, S2, S1

Possible Problem: Polygons that alternately obscure one another. Kemungkinan Soal: Poligon yang jelas bergantian satu sama lain. These three polygons will continuously reorder. Ketiga poligon akan terus menyusun ulang.

Satu solusi mungkin untuk bendera yang mengatur kembali dan membagi poligon poligon menjadi beberapa poligon yang lebih kecil.



di kutip dari www.siggraph.org/education